MATRIZES

Introducción

Las matrices son herramientas muy usadas en matemáticas, computación, física, economía y muchas otras áreas. Sirven para organizar datos y resolver sistemas de ecuaciones. Puedes imaginarlas como tablas de números que permiten hacer operaciones fácilmente.

---

Definición

Una matriz es una colección de números ordenados en filas y columnas. Cada número que está en una matriz se llama elemento.

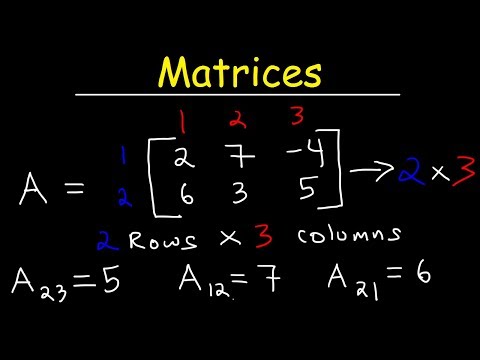
Por ejemplo, esta es una matriz de 2 filas y 3 columnas:

$$\begin{pmatrix} 1 & 4 & 7 \\ 2 & 5 & 8 \end{pmatrix}$$

---

Notación

Una matriz generalmente se representa con una letra mayúscula como $A$, $B$, $M$, etc.

• Se escribe como $A_{m \times n}$, donde:

  • $m$ es el número de filas

  • $n$ es el número de columnas

Por ejemplo, si una matriz tiene 2 filas y 3 columnas, se dice que es una matriz $2 \times 3$.

Cada elemento se identifica como $a_{ij}$, donde:

• $i$ es el número de fila

• $j$ es el número de columna

---

Aritmética Matricial

Suma de matrices

Solo se pueden sumar matrices del mismo tamaño.

Ejemplo:

$$A = \begin{pmatrix} 1 & 2 \\ 3 & 4 \end{pmatrix}, \quad B = \begin{pmatrix} 5 & 6 \\ 7 & 8 \end{pmatrix}$$ $$A + B = \begin{pmatrix} 1+5 & 2+6 \\ 3+7 & 4+8 \end{pmatrix} = \begin{pmatrix} 6 & 8 \\ 10 & 12 \end{pmatrix}$$

---

Multiplicación de matrices

Se puede multiplicar una matriz $A_{m \times n}$ con una matriz $B_{n \times p}$. O sea, el número de columnas de la primera debe coincidir con el número de filas de la segunda.

Ejemplo:

$$A = \begin{pmatrix} 1 & 2 \\ 3 & 4 \end{pmatrix}, \quad B = \begin{pmatrix} 5 & 6 \\ 7 & 8 \end{pmatrix}$$

Multiplicación:

$$AB = \begin{pmatrix} (1×5 + 2×7) & (1×6 + 2×8) \\ (3×5 + 4×7) & (3×6 + 4×8) \end{pmatrix} = \begin{pmatrix} 19 & 22 \\ 43 & 50 \end{pmatrix}$$

---

Matriz Identidad

Es una matriz cuadrada (mismo número de filas y columnas) que tiene unos en la diagonal principal (de arriba a la derecha) y ceros en los demás lugares.

Ejemplo de matriz identidad $3 \times 3$:

$$I = \begin{pmatrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{pmatrix}$$

Es como el número 1 para las matrices, porque multiplicar una matriz por la identidad no la cambia:

$$A \cdot I = A$$

---

Matriz Transpuesta

La transpuesta de una matriz es una nueva matriz que se obtiene intercambiando filas por columnas.

Ejemplo:

$$A = \begin{pmatrix} 1 & 2 & 3 \\ 4 & 5 & 6 \end{pmatrix} \Rightarrow A^T = \begin{pmatrix} 1 & 4 \\ 2 & 5 \\ 3 & 6 \end{pmatrix}$$

​